Ein zentraler Begriff der Analysis ist der Begriff der Monotonie bzw. der strengen Monotonie.
Eine Funktion f heißt auf einem Intervall I streng monoton steigend, wenn für x1 < x2 folgt, dass f(x1) < f(x2)
Eine Funktion f heißt auf einem Intervall I streng monoton fallend, wenn für x1 < x2 folgt, dass f(x1) > f(x2).
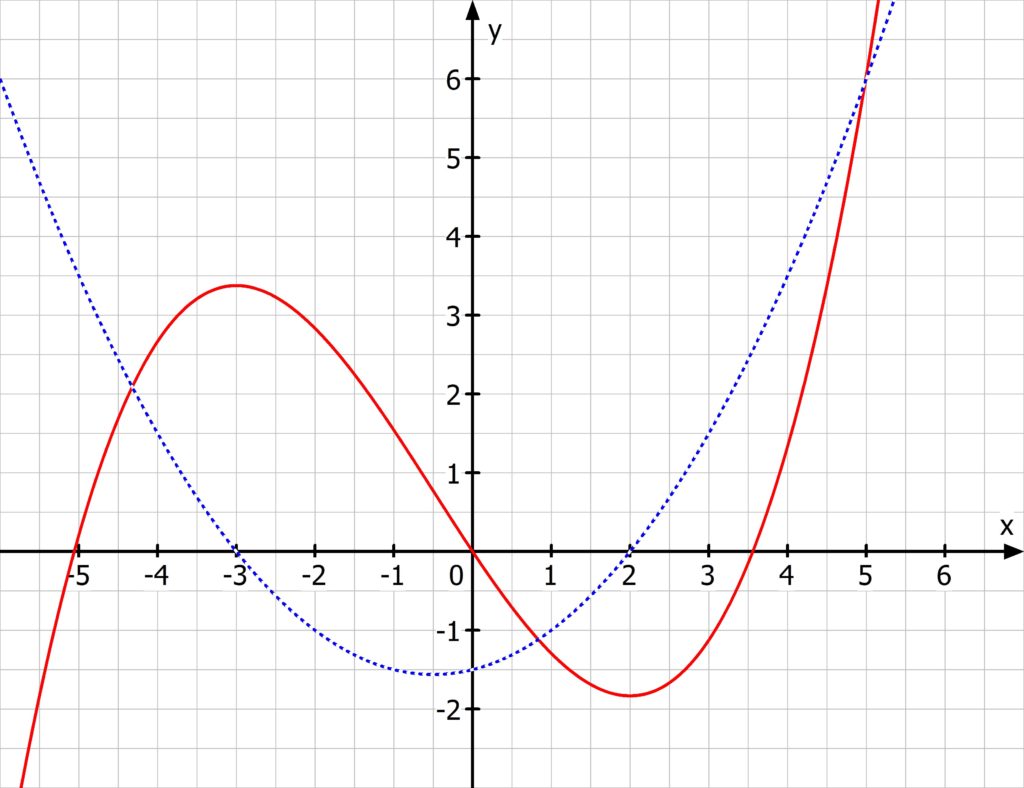
Betrachtet man den Graphen der roten Funktion f, so erkennt man, dass für x<-3 f streng monoton steigt. Für -3<x<2 ist f streng monoton fallend und für x>3 ist f streng monoton steigend.
Es fällt auf, dass f´ (blauer Graph) für x<-3 größer als null ist, für -3<x<2 kleiner als null ist und für x>2 wieder positiv ist!
Dies mündet im sogenanten Monotoniesatz
Ist eine Funktion f differenzierbar auf einem Intervall I und
ist f´(x) > 0, dann ist f streng monoton steigend
ist f´(x)<0, dann ist f streng monoton fallend.
Ein Blick auf den Graphen der Funktion f(x)=x3 zeigt, dass die Umkehrung des Satzes leider falsch ist, denndie erste Ableitung wird an der Stelle x=0 null obwohl f eine streng monoton wachsende Funktion ist!
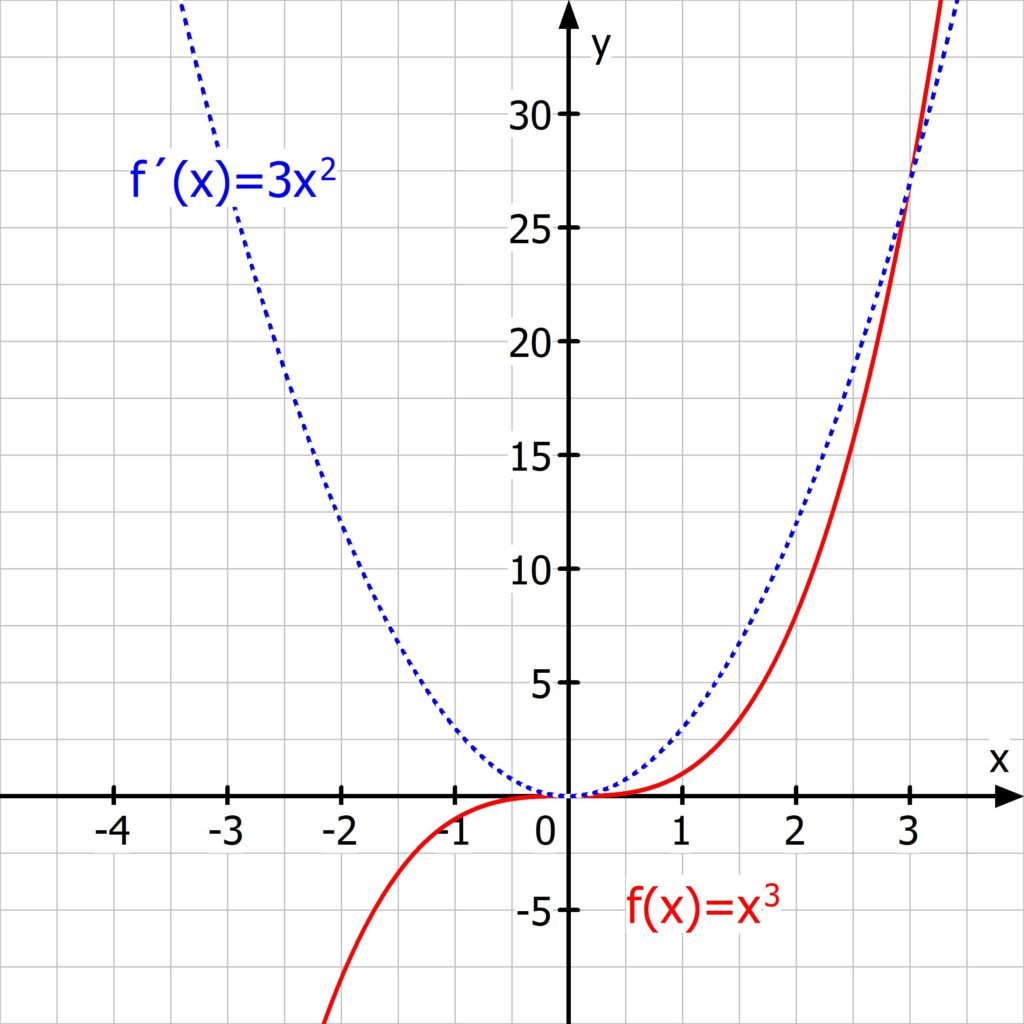
Man kann also vom Vorzeichen von f´ auf das Monotonieverhalten von f schließen aber eben leider nicht umgekehrt!
Wir führen den Beweis für den Fall f´(x0) > 0 . Der Fall f´(x0) < 0 verläuft analog.
Sei also f´(x0) > 0. Man wählt eine h Umgebung von x0 Uh(x0)
| Für h > 0 gilt dann das x0<x0+h und nach Voraussetzung
\[ \lim \limits_{h \to \ 0}{\frac{f(x_0+h)-f(x_0)}{h}} > 0 \] \[ \Rightarrow \frac{f(x_0+h)-f(x_0)}{h} > 0 \] Multipliziert man mit h, dann ergibt sich \[ \Rightarrow f(x_0+h)-f(x_0) > 0 \]
also \[ f(x_0+h)> f(x_0) \] somit ist f streng monoton steigend, da ja h > 0 war |
Für h < 0 gilt dann das x0 > x0+h und nach Voraussetzung
\[ \lim \limits_{h \to \ 0}{\frac{f(x_0+h)-f(x_0)}{h}} > 0 \] \[ \Rightarrow \frac{f(x_0+h)-f(x_0)}{h} > 0 \] Multipliziert man mit h < 0 ergibt sich \[ \Rightarrow f(x_0+h)-f(x_0) < 0 \] (Beachte das Ungleichheitszeichen ändert sich, da h < 0) also \[ f(x_0+h)< f(x_0) \] somit ist f streng monoton steigend, da ja h < 0 war |
Für alle h ist also f streng monoton steigend, was zu beweisen war.
