Der Begriff der Differenzierbarkeit. Eine Funktion f heißt differenzierbar an einer Stelle x0, wenn der Grenzwert des Differenzenquotienten existiert, wenn also
\[ \lim \limits_{h \to \ 0}{\frac{f(x_0+h)-f(x_0)}{h}} \]
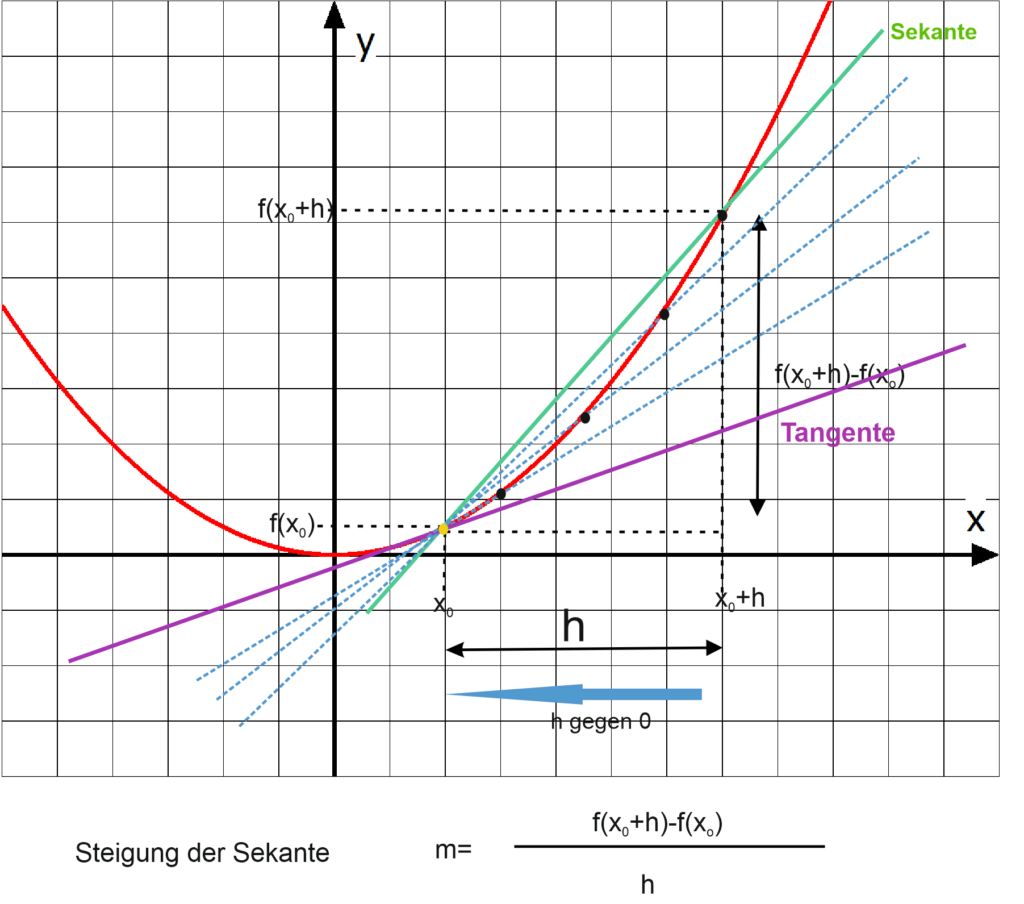
für h gegen null existiert. Anders ausgedrückt, die Steigung der Sekante nähert sich für h -> 0 immer mehr der Steigung der Tangente (siehe Abbildung). Den Grenzwert des Differenzenquotienten nennt man Ableitung f´ von f.
\[ f´(x_0)\ = \lim \limits_{h \to \ 0}{\frac{f(x_0+h)-f(x_0)}{h}} \]
Betrachten wird die Funktion \[ f(x)=5x^2-3x+4 \].
\( f´(x_0)\ = \lim \limits_{h \to \ 0}{\frac{f(x_0+h)-f(x_0)}{h}} = \lim \limits_{h \to \ 0}{\frac{[5\cdot (x_0+h)^2)-3(x_0+h)+4]-(5x_0^2-3x_0+4)}{h}} \)
\( = \lim \limits_{h \to \ 0}{\frac{5(x_0^2+2x_0h+h^2)- 3x_0-3h+4-5x_0^2+3x_0-4}{h}}= \lim \limits_{h \to \ 0}{\frac{5x_0^2+10x_0h+5h^2-3x_0-3h+4-5x_0^2+3x_0+4}{h}} \)
\( =\lim \limits_{h \to \ 0} { \frac {10\cdot x_0h+5\cdot h^2-3h }{h} }=\lim \limits_{h \to \ 0} \frac{ \require{cancel} \cancel{\text{h}} \cdot (10 \cdot x_0+5 \cdot h-3)} {\require{cancel} \cancel{\text{h}}}= \lim \limits_{h \to \ 0} 10 \cdot x_0+ \underbrace{5\cdot h}_{gegen\ null für\ h -> 0 } -3 =10\cdot x_0-3 \)
Folglich ist die Funktion f differenzierbar und es gilt:
\[ f´(x)=10x-3 \]
Dabei beschreibt die Ableitung von f also f´ die Steigung von f in jedem Punkt. Will man also wissen, welche Steigung f an der Stelle x = -1 hat, so muss man -1 in f´(x) einsetzen und man erhält
\[ f´(-1)\ =10 \cdot (-1)-3=-33 \] Die Steigung an der Stelle x=-1 ist also m=-33
Hier ein Beispiel einer Funktion, die nicht überall differenzierbar ist.
\[ f(x)=| x | = \begin{cases} +x & \text{ falls } x > 0 \\ \;\;0 & \text{ falls } x = 0 \\ -x & \text{ falls } x < 0 \end{cases} \]
ist an der Stelle x0 = 0 nicht differenzierbar.

\( \lim \limits_{h \to \ 0+}{\frac{f(x_0+h)-f(x_0)}{h}}=\lim \limits_{h \to \ 0+}\frac{\left|x_0+h\right|\ -\ x_0}{h}\ {\underbrace{=} _{h >0}} \lim \limits_{h \to \ 0}\frac{0+h\ -0\ }{h}=\lim \limits_{h \to \ 0}\frac{h}{h}\ =\ 1 \)
\( \lim \limits_{h \to \ 0-}{\frac{f(x_0+h)-f(x_0)}{h}}=\lim \limits_{h \to \ 0-}\frac{\left|x_0+h\right|\ -\ x_0}{h}\ {\underbrace{=} _{h < 0}} \lim \limits_{h \to \ 0-}\frac{0-h\ -0\ }{h}=\lim \limits_{h \to \ 0}\frac{-h}{h}\ =\ -1 \)
Linker und rechter Grenzwert stimmen also an der Stelle Null nicht überein und liefern unterschiedliche Werte, also exisiert der Grenzwert nicht bzw. ist nicht eindeutig. Die Funktion ist also an der Stelle x0 = 0 nicht differenzierbar.
